How does a neuron really *fire*?
But what is a neuron? Think of a neuron as the fundamental unit of processing in our brains. Analogous to transistors in a microcontroller or a processing unit, neurons, when connected intelligently together, can form rather intricate circuits that perform logic and computation quickly and efficiently . Zooming in on these circuits, a neuron receives inputs and decides whether to pass them to other neurons or not. However, this process is not as straight forward as it might first sound; there is a multitude of intertwined variables at play that dictate this process on the single neuron level. Let’s take a deeper look into what makes up a neuron.
The anatomy of a neuron
A neuron, without loss of generality, is made up from a cell body connected to dendrites and an axon. Dendrites serve as the input site to the neuron and the axon is where the signal travels before it is outputted onto other neurons’ dendrites. However, like other cells in our body, a neuron is made up from a membrane that contains the organs of the neuron -or organelles- that perform the necessary function to keep the neuron alive. This membrane as we’ll see plays a critical role in the neuron’s ability to generate and conduct electrical signals.
The Membrane:
Cell membranes are known as a ‘Phospholipid Bilayer’. As the name suggests, a patch of membrane is made up from lots of repeating molecules called ‘Phospholipids’ stacked next to one another. Each of these molecules contains a phosphate head and two fatty acid tails. For the membrane to be doing its job, it has to act as a barrier isolating the inside (intracellular space) of the cell from the outside (extracellular space). Both of these spaces contain lots of water. Now the phosphate head likes to be in contact with water and hence it is called ‘hydrophilic’, while the fatty acid tails are repelled from water and called ‘hydrophobic’. Due to this dichotomous property, if we add these molecules to water, they will arrange themselves in such a way that ‘protects’ the tails from water, while exposing the head to water. One possible arrangement, as you can imagine, is for every two phospholipid molecules to align their fatty acid tails facing one another hiding them from water. This gives the rise to a bilayer sheet of phospholipids - or a phospholipid bilayer.
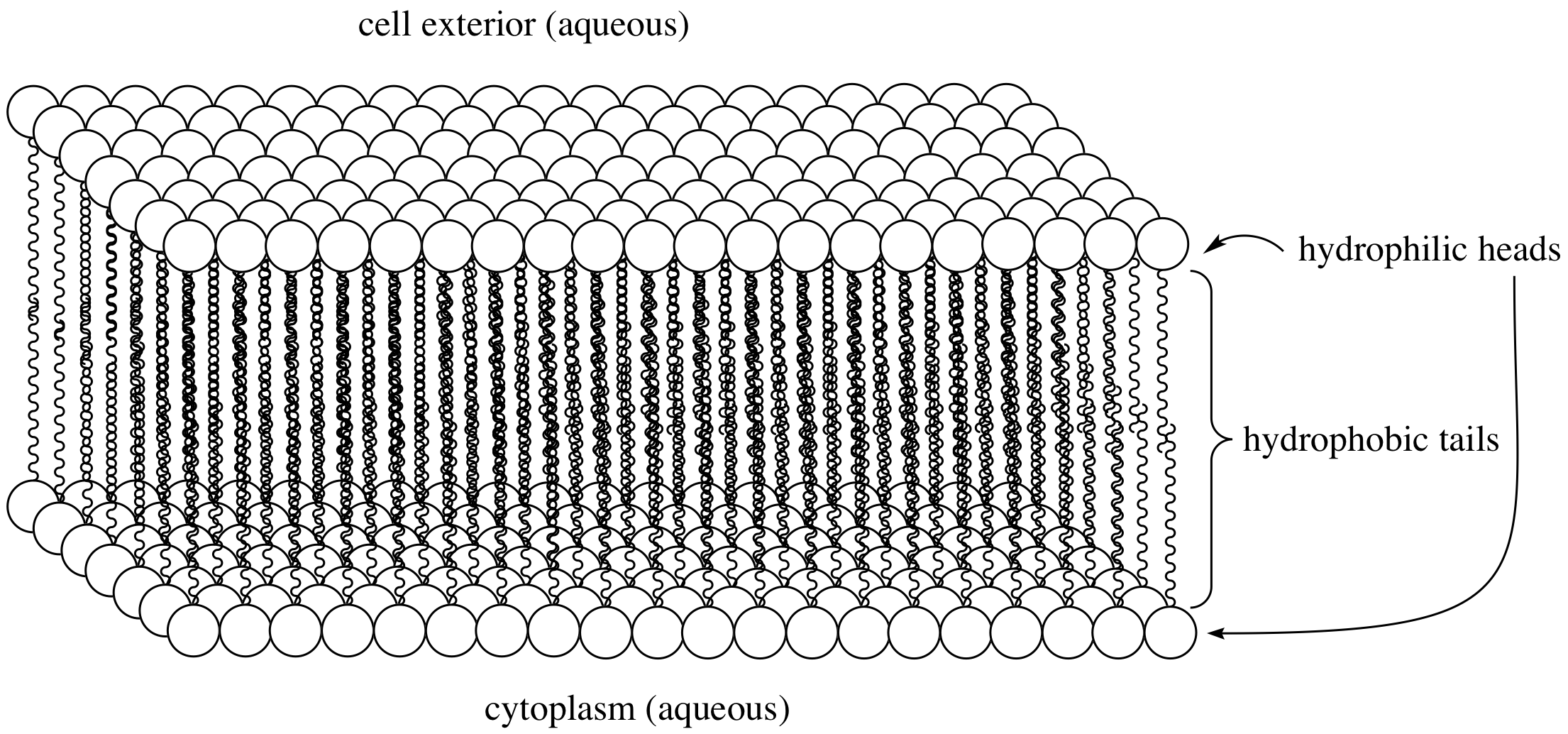
Adapted from chem.UCLA
Although it might not seem like it, but the molecules in this resulting structure -the membrane- are very tightly packed together, so no molecules or ions can pass through the membrane. Instead, there are channels that the cell produces and embeds within the membrane to act like a tunnel for ions to pass through in and out of the cell. The result therefore is a semi-permeable membrane -only permeable to select ions to pass- while blocking the passage of all other species. This is where all the magic starts!
Nernst and the ionic tug of war
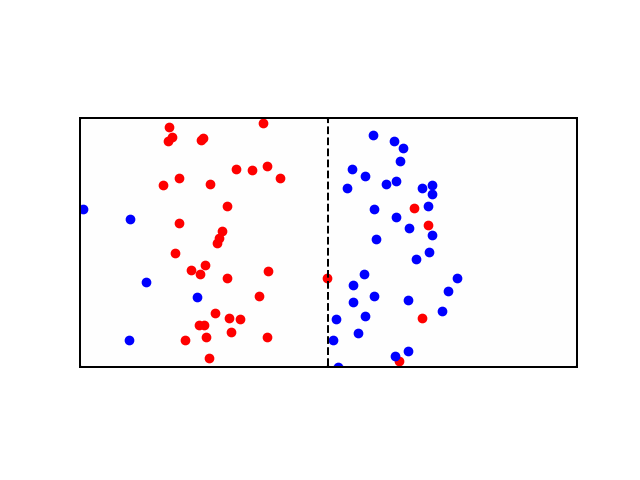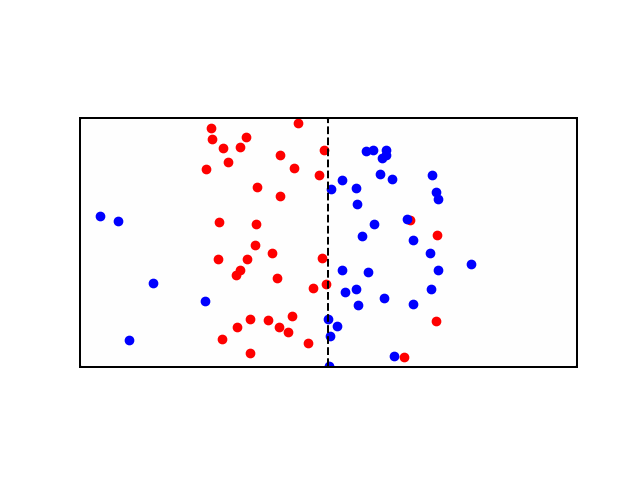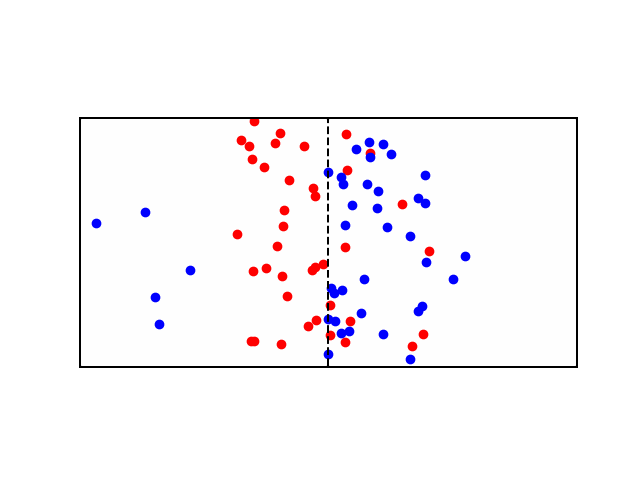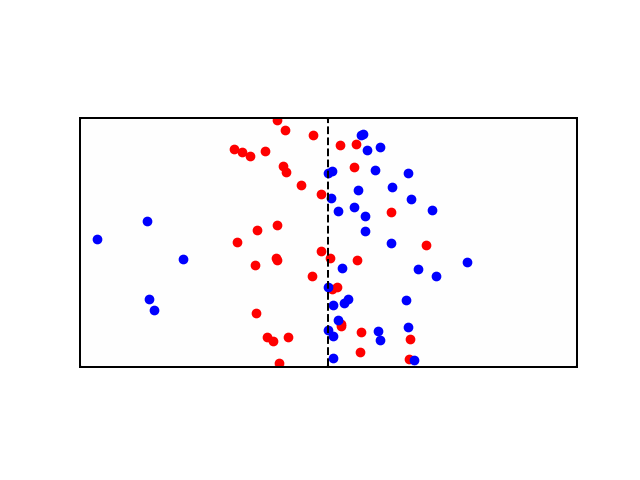
Consider a didactic square container divided in the middle by a similar semi-permeable membrane forming Compartment \(A\) and Compartment \(B\). Each Compartment contains a solution containing different concentrations of molecule \(X\) and molecule \(Y\). Let there be more \(X\) in compartment \(A\) and more \(Y\) in compartment \(B\). In other words: \([X]_A > [X]_B\) and \([Y]_B > [Y]_A\). If the membrane is permeable to \(X\), then \(X\) will flow from \(A\) to \(B\) along the concentration gradient until the concentration is equalized. See animation below: red particles diffuse freely to the right compartment until the gradient is equalized.
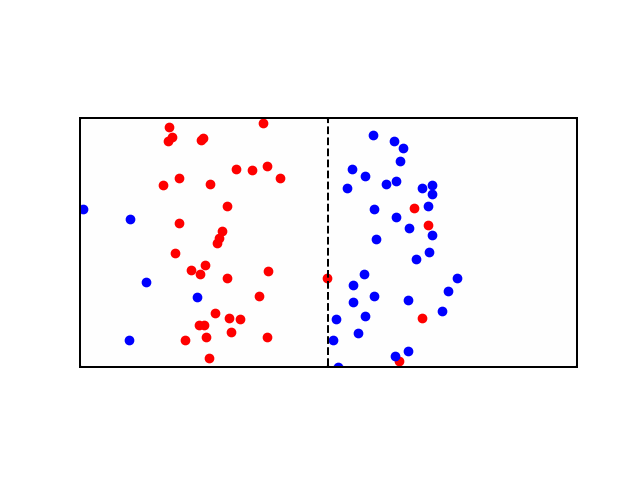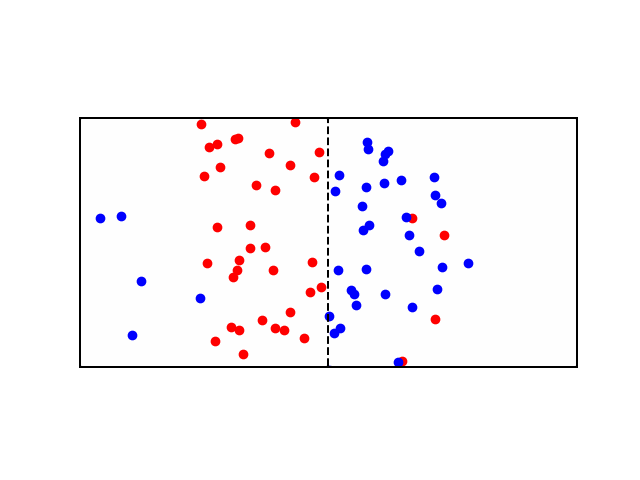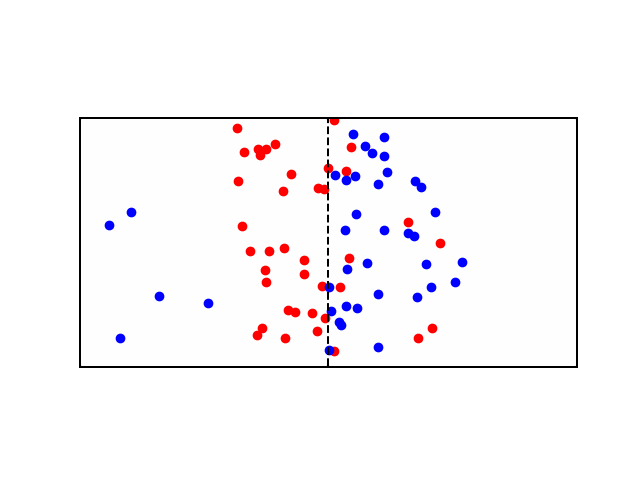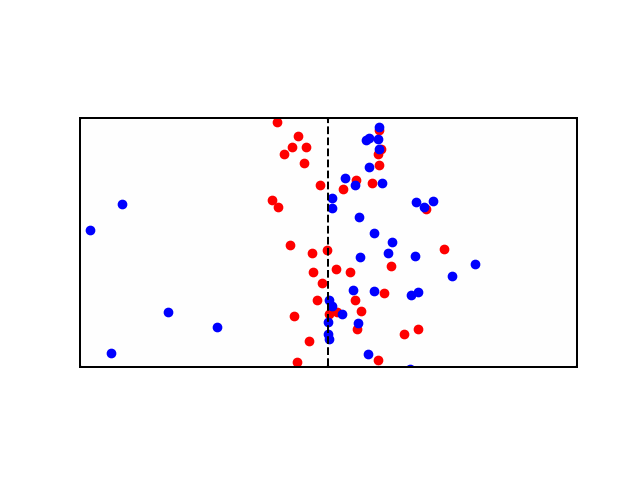
But what if \(X\) and \(Y\) have a charge? say \(X^+\) and \(Y^+\). Well now \(X^+\) will flow from \(A\) to \(B\) as before, but as more of it flow to \(B\), they experience a repelling force from all the other positive ions in \(B\). Moreover, now that \(A\) has less positive ions than \(B\), it is relatively negative to \(B\), meaning that \(X^+\) ions also experience an attractive force pulling them back to \(A\). Therefore there are two gradients at play here, diffusion gradient, and electrochemical gradient. When these two gradients are equal, the system is said to have reached equilibrium and the resulting potential difference between compartments \(A\) and \(B\) is called the Equilibrium Potential. At this state, the number of \(X^+\) leaving \(A\) due to the concentration gradient is equal to the number of \(X^+\) entering \(A\) due to the electrical gradient - see animation below: as more red particles move to the right side, they start to experience an attraction force back towards the left side.
This quantity can be calculated by what is known as the Nernst equation: $$E = E_{\text{eq}} + \frac{RT}{zF} \ln\left(\frac{[C_{\text{in}}]}{[C_{\text{out}}]}\right)$$
Without going into the details of the equation, the equilibrium potential is mainly decided by the valence of the ion \(z\)- or the charge- and the ratio of its concentrations on both sides of the membrane. You can probably tell that this is the beginning of some sort of an electrical signal, but how does this signal originate and propagate if we’re always at the equilibrium potential \(E\) ? In one word: Channels
Channels Channels Channels!
Well, more like three words: voltage-sensitive channels.
So far we’ve only considered one ionic species crossing the membrane. But what if by the flip of a switch, the membrane becomes permeable to \(Y^+\) too? Well then \(X^+\) has an \(E_{eq}^{X^+}\) associated with it and \(Y^+\) has an \(E_{eq}^{Y^+}\) associated with it. Once we flip the switch, the voltage across the membrane will start to shift from \(E_{eq}^{X^+}\) towards \(E_{eq}^{Y^+}\), not quite reaching it but towards its direction. Goldman, Hodgkin, and Katz figured out how to calculate the equilibrium potential with the membrane permeable to multiple ions - lookup GHK Equation.. Now we can see that by somehow changing the permeability of the membrane to certain ionic species, we can generate a transient in the potential difference across its both sides! Let us now bring it back to the biological neuron.
The neuron’s intracellular space - the lumen - is concentrated with Potassium ions \(K^+\), while the extracellular space surrounding the neuron is deficit in \(K^+\) but rich in Sodium \(Na^+\). Think of a banana covered in salt whenever you want to remember which side is rich in what. The neuronal membrane has \(K^+\) and \(Na^+\) channels that allow \(K^+\) and \(Na^+\) to pass through, respectively. These channels can be opened and closed to different levels, therefore changing the relative permeability of each of the ionic species. At rest, approximately half of the \(K^+\) channels are open, meaning that \(K^+\) is leaking out of the neuron and the membrane’s potential sits close to \(E_{eq}^{K^+} \approx -75mV \). Remarkably, these channels are voltage-sensitive, or voltage-gated, meaning that the potential difference dictates membrane permeability, and membrane permeability in turn dictates membrane potential difference! For example, \(Na^+\) channels open at around \(-55mV\) and inactivates \(\approx 0mV\). \(K^+\) open around \(0-20mV\) and start closing upon repolarization. Given all of that, let us zoom in on a single firing event from a neuron:
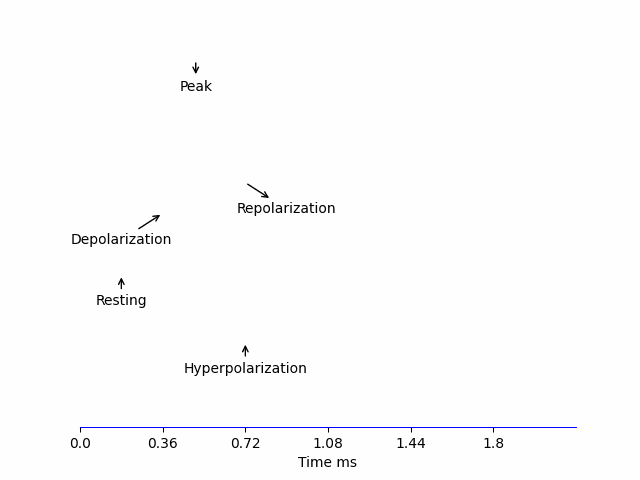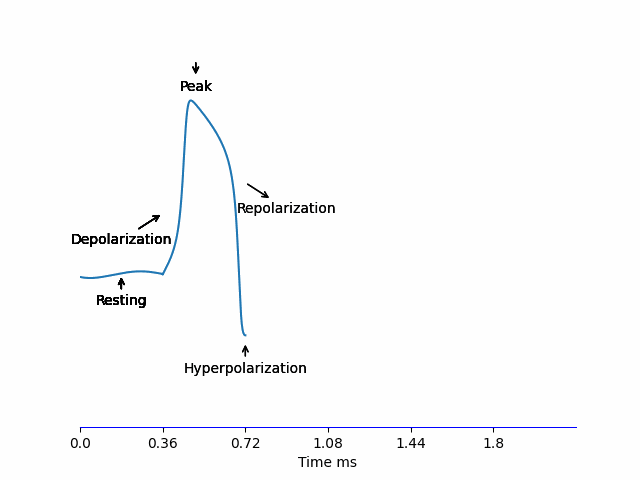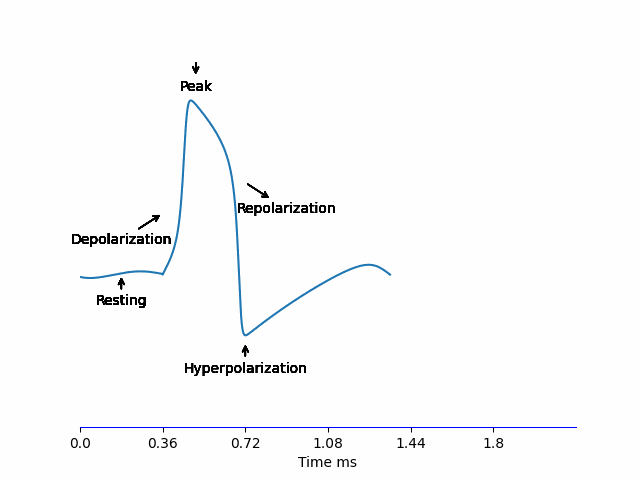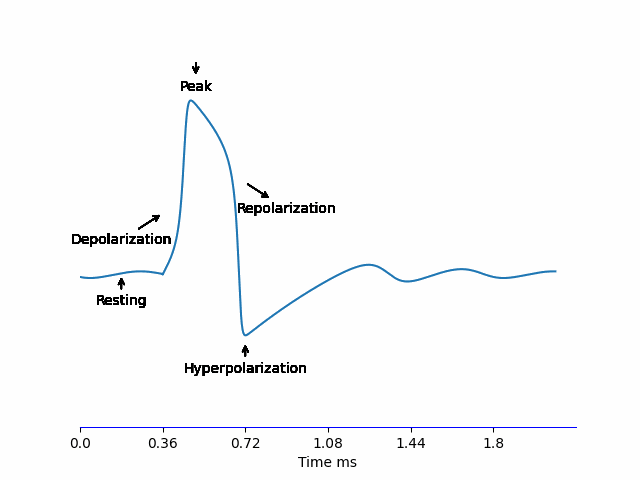
When a neuron receives an input -we’ll discus this in more detail later on, but for name let’s say it’s some electric current being injected- the potential difference of the membrane \(V_m\) increases. If it reaches the threshold \(\approx -55mV\), an Action Potential is generated according to the steps below:
- Depolarization: The voltage-sensitive \(Na^+\) channels to open allowing \(Na^+\) to rush into the neuron increasing \(V_m\) very quickly to reach the peak \(\approx 30mV\).
- Repolarization: At this high \(V_m\), \(K^+\) channels are opening, allowing \(K^+\) to rush out of the neuron and \(V_m\) starts decreasing bringing it down to \(V_m^{resting}\). But these channels are slow, so the Repolarization stage is relatively long.
- Hyperpolarization: Because of the slow dynamics of the \(K^+\) channel, it doesn’t fully close in time at \(V_m^{resting}\), so \(V_m\) continues decreasing and overshoots the normal \(V_m^{resting} = -70mV\) reaching \(-80mV\) before \(K^+\) close and the membrane voltage recovers back to normal.
All of this happens in less than 2ms!
Notice how channels and their voltage sensitivity play the critical role of generating Action Potentials, the basic alphabet of neuronal language. Wouldn’t it be great if we could model how these channels open and close? We can then predict how the neuron will react to a certain input. Alan Hodgkin and Andrew Huxley set out to do this in the 1940s by recording from the squid giant axon. As a result of their work, the Hodgkin-Huxley (H-H) model was born and they both won A Nobel Prize.
Channels have doors? <in progress>
Well, gates. Channels have gates. The \(Na^+\) channels have two gates. An activation gate, which opens when the membrane potential crosses the threshold, and an inactivation gate which closes after a certain time (tiny tiny amount of time, fraction of a millisecond) stopping \(Na^+\) from entering the neuron. At rest, the activation gate is closed and the inactivation gate is open, no \(Na^+\) flow is allowed. When the threshold is crossed, the activation gate opens, both gates are now open and \(Na^+\) can flow. After some tiny amount of time, the inactivation gate closes stopping the \(Na^+\) flow. When the neuron relaxes back to rest, the activation gate closes. A little after that, the inactivation gate re-opens and the neuron is now ready to fire again. The voltage-gated \(K^+\) channels have one gate that opens when \(V_m\) crosses \(-50mV\), but they are slow compared to \(Na^+\) activation gates. This delay allows for the \(Na^+\) peak we see in the Action Potential.
The H-H model describes the opening and closing dynamics of these gates using a set of differential equations. Refer to this great EPFL resource for a deeper dive into the H-H model. Then use my simulation and graphical interface to see how different input amplitudes and timings result in action potentials. You can also change the properties of the channels, add more channels, and experiment with how they affect the overall response of the neuron. See example below:
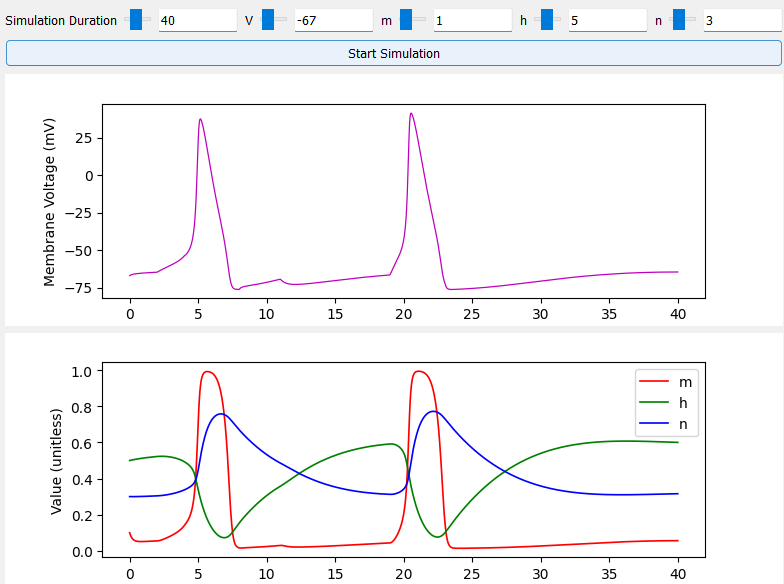
My simulation uses membrane and channel properties approximated by: Svirskis, G., Kotak, V., Sanes, D.H. and Rinzel, J., 2004. Sodium along with low-threshold potassium currents enhance coincidence detection of subthreshold noisy signals in MSO neurons. Journal of neurophysiology, 91(6), pp.2465-2473. Simulation code was written with guidance from Professor Laurel Carney during my undergraduate days at the University of Rochester.